Into the Wild: Machine Learning In Non-Euclidean Spaces
Is our comfortable and familiar Euclidean space and its linear structure always the right place for machine learning? Recent research argues otherwise: it is not always needed and sometimes harmful, as demonstrated by a wave of exciting work. Starting with the notion of hyperbolic representations for hierarchical data two years ago, a major push has resulted in new ideas for representations in non-Euclidean spaces, new algorithms and models with non-Euclidean data and operations, and new perspectives on the underlying functionality of non-Euclidean ML. We review some of these exciting ideas, describe some of our contributions, and provide a vision into the future of non-Euclidean space (the final frontier?).
Check out our papers: ICML '18, ICLR '19, NeurIPS '19, GR Learning '19 (fresh off the presses!), and our code on GitHub!
Machine learning (ML) methods have become enormously successful and popular. Their rise to fame and fortune has occurred via evolution: a gradual grafting of ideas and approaches contributed by many thinkers and spanning many fields onto the overall structure. While this approach has produced a robust field, it has also led to several key notions to be de-facto adopted into the machine learning ecosystem for reasons of convenience or tradition, rather than by design. One important such choice has to do with geometry, and it is the subject of this blog post.
Geometry is certainly not an unfamiliar field for the ML community; geometric ideas play an important role in many parts of ML. For example, we often study the convexity landscapes of functions, dimensionality and projections are critical to data representations, and we frequently produce visualizations to understand our data and training processes. At the same time, these geometric notions are typically thought of as specific properties of some aspects of ML. However, geometry is far more pervasive and fundamental than these particular properties.
The core object in the ML pipeline is the vector, or, alternatively, its multidimensional generalization, the tensor. Indeed, it is so fundamental that it lends its name to one of the most successful ML frameworks. It is perhaps to be expected that this is the case---the natural choice for an operable representation of data is to produce a vector or matrix of real numbers. By doing so, however, we have already imposed a choice of geometry. We have chosen to work with Euclidean space, with all of its inherent properties, among the most critical of which is its flatness.
Why is this a problem? As described by Bronstein et al. in their seminal description of the geometric deep learning paradigm, "[m]any scientific fields study data with an underlying structure that is a non-Euclidean space." Just a few reasons to abandon our comfortable old workhorse vector spaces:
- Better representations: Euclidean space simply doesn't fit many types of data structures that we often need to work with. The core example is the hierarchy, or, its abstract network representation, the tree. More than that---there is a specific non-Euclidean choice that naturally fits trees: hyperbolic space, as showed by Nickel and Kiela and Chamberlain et al. in their exciting papers. We have a good understanding of the tradeoffs involved in hyperbolic representations. More flexible spaces---like mixed-curvature products---provide enough expressivity for other, less regular, types of data,
- Unlocking the full potential of models: there are a proliferation of increasingly sophisticated models coming out daily. What are the limits governing the performance of these models? We argue that the space the points live in can be one such limit, and that if we lift these models (both the space and functions) to the non-Euclidean versions, in certain cases we can break through these limits. Our recent work suggests that this is the case with graph convolution networks (GCNs), in particular in the scenario where our datasets are hyperbolic-like, like PubMed. Tifrea et al. likewise reach SoTA for word hypernymy tasks using hyperbolic word embeddings.
- More flexible operations: The flatness of Euclidean space means that certain operations require a large number of dimensions and complexity to perform---while non-Euclidean spaces can potentially perform these operations in a more flexible way, with fewer dimensions. Our preliminary ideas show how to put these notions to use in knowledge graph embeddings.
In the rest of this post, we describe some of these ideas and provide some perspective on what (we think) is next. While many of these notions might seem exotic, we offer code implementing them, bringing them down to earth. You can train and explore your own non-Euclidean representations and models!
Limitations of a Flat World
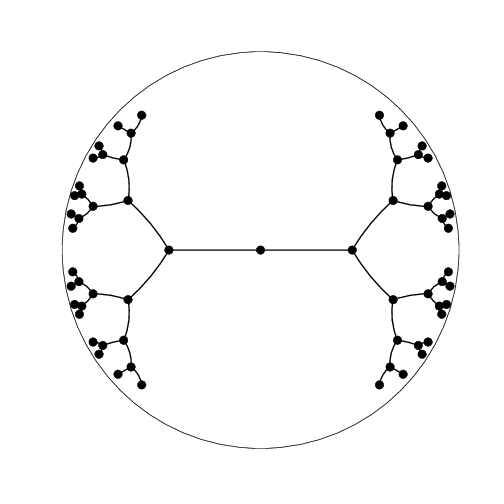
The canonical example of why Euclidean geometry isn't quite sufficient involves representations for hierarchies, and this example motivated the use of hyperbolic space for graph representation learning in ML. Two exciting papers made this point: Nickel and Kiela and Chamberlain et al., kicking off the area. These works sought to produce a graph embedding, preserving the structure of the graph. Trees are used in particular, as they represent hierarchical relationships.
This seemingly simple idea has wide applicability: there are hierarchical relationships in many places, such as lexical databases like WordNet, Wikipedia categories, biological and chemical taxonomies such as phylogenetic relations, knowledge graphs like Freebase, and many others. Exploiting all of these with a machine learning model necessitates continuous representations, and so we must embed a tree into a continuous space.
What properties do we need to embed a tree (or any graph) well? Specifically, we want to maintain the distances of nodes in the tree when these are embedded. Thus we’d like the embedded versions of a pair of sibling nodes to be at distance 2, an embedded node and its parent to be at distance 1, and so on. However, we might need a lot of ‘room’ for this: in a binary tree, each additional layer of depth has twice as many nodes as the previous layer. That is, the ‘volume’ growth of the tree is exponential in the tree depth.
What is the continuous version of this counting argument? Ideally, we’d like a ball whose volume grows exponentially in the radius. This doesn’t happen in Euclidean space (recall, for example, the formula for the volume of a 3D sphere: \(V = 4/3 \pi r^3\), which is just polynomial). But in fact, hyperbolic space offers exactly this property---which makes for great embeddings, and we're off!
But before we can run, we must walk. We start with the basics:
Getting it To Work in ML: Differential Geometry
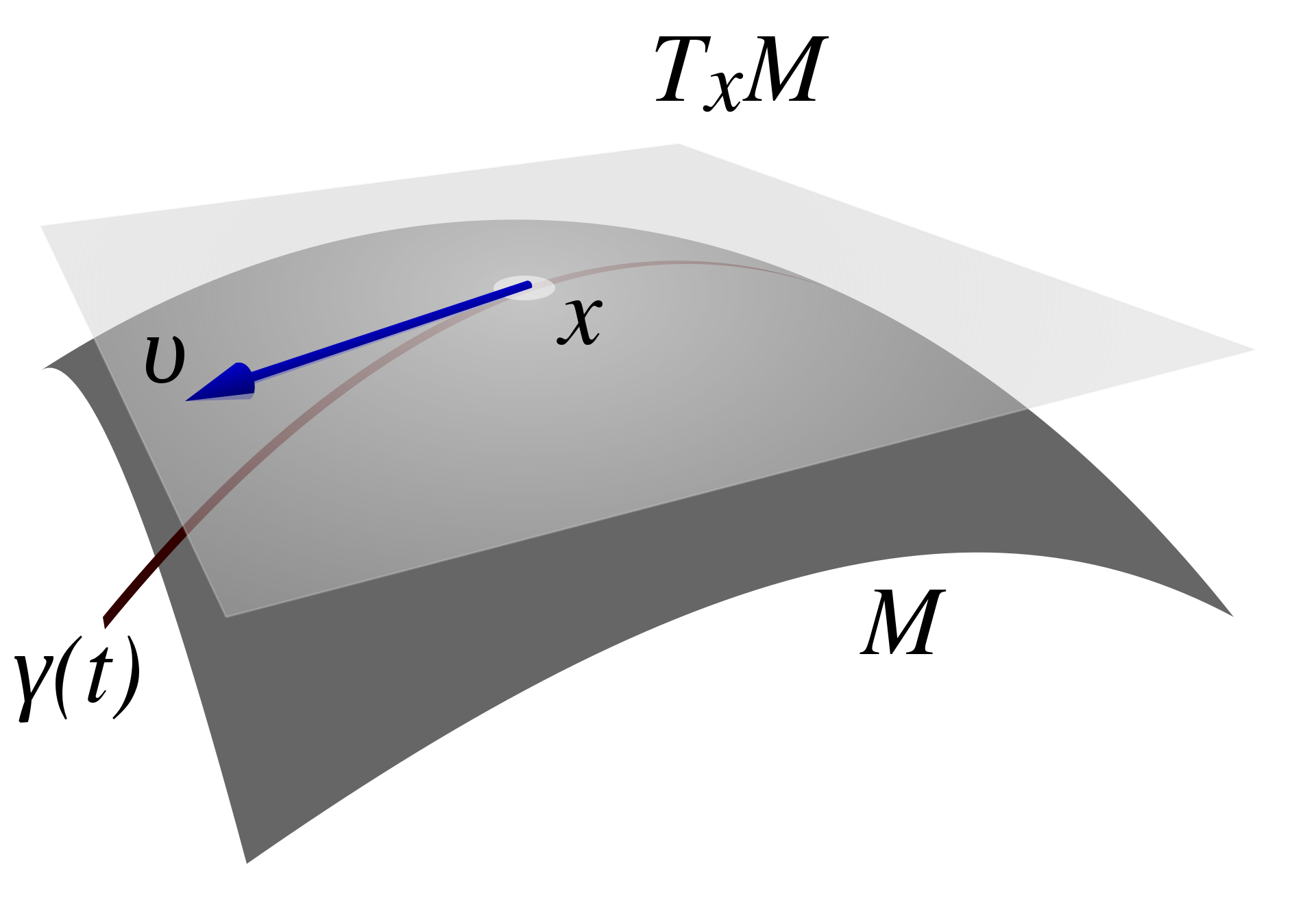
Perhaps the biggest difficulty with dropping our unhealthy addiction to Euclidean space is simply how to make it work. This can be hard---but the benefits are worth it! Hyperbolic space is one type of more general space called a manifold. Then our goal is to replace \(\mathbb{R}^n\) with the \(n\)-dimensional manifold \(\mathcal{M}\). What do we need for our ML tasks?
- A model: this is a function \(f:\mathcal{M} \rightarrow \mathcal{M}\) and a way to evaluate that function, that is, to compute \(f(p)\) for \(p \in \mathcal{M}\),
- A way to train our model, equivalent to computing derivatives for \(f\) and taking steps,
- An embedding space, that is a choice of Euclidean or non-Euclidean geometry that, in a sense, corresponds to the input data.
Fortunately, mathematicians have spent a couple of centuries (since Gauss!) figuring out how to do this for us. The field of differential geometry has the answers we need. It tells us how to define meaningful differentiable (smooth) functions on \(\mathcal{M}\) and how to do calculus with them.
Below we very briefly review some key ideas. Lots of resources offer a much deeper treatment, for example Loring Tu's and Jack Lee's books on manifolds.
A manifold \(\mathcal{M}\) is an object that looks like \(\mathbb{R}^n\), but only locally. That is, \(\mathcal{M}\) can be written as the union of a collection of charts, which are smooth bijective mappings between (open) subsets of \(\mathcal{M}\) and open subsets of \(\mathbb{R}^n\). Continuing the naval analogy, a set of charts covering \(\mathcal{M}\) is an atlas. Charts enable us to work with local coordinates, which means we can fortunately write down points and operate with them---but only for a chart!
Calculus naturally involves linear approximations at each point of the manifold. These linear approximations involve tangent spaces; the objects living in each tangent spaces are tangent vectors. There are many ways to understand tangent vectors, from the abstract to the concrete, but for our setting, we can think of them as generalizations of velocity vectors for functions. We frequently flip between these vectors and points on the manifold itself. A pair of functions allow us to do so: the \(\exp\) map takes us from the tangent space to the manifold, and the \(\log\) map gives the reverse. Now we can do calculus in our manifolds!
Finally, we equip our manifolds with a special type of "ruler", called a Riemannian metric. This metric, which is itself a function that may vary at each point, enables us to measure inner products between tangent vectors. This allows us to express geometric quantities (e.g., angles, lengths, and distances), and talk about shortest paths, called geodesics.
And that's it! The outcome of these generalizations enables us to do all the things we’d like to do for training ML models. Among a few examples, we can train with optimizers:
- Bonnabel introduced Riemannian SGD,
- Zhang, Reddi, and Sra added Riemannian SVRG,
- Wilson and Leimeister studied the fundamentals of gradient descent in hyperbolic space,
- Becigneul and Ganea developed Riemannian ADAM.
- with non-Euclidean parameters,
- or even more general hyperbolic neural networks as in Ganea, Bécigneul, Hofmann.
Now we’re ready for our first task—embedding trees into hyperbolic space.
Getting Hyperbolic About Embeddings
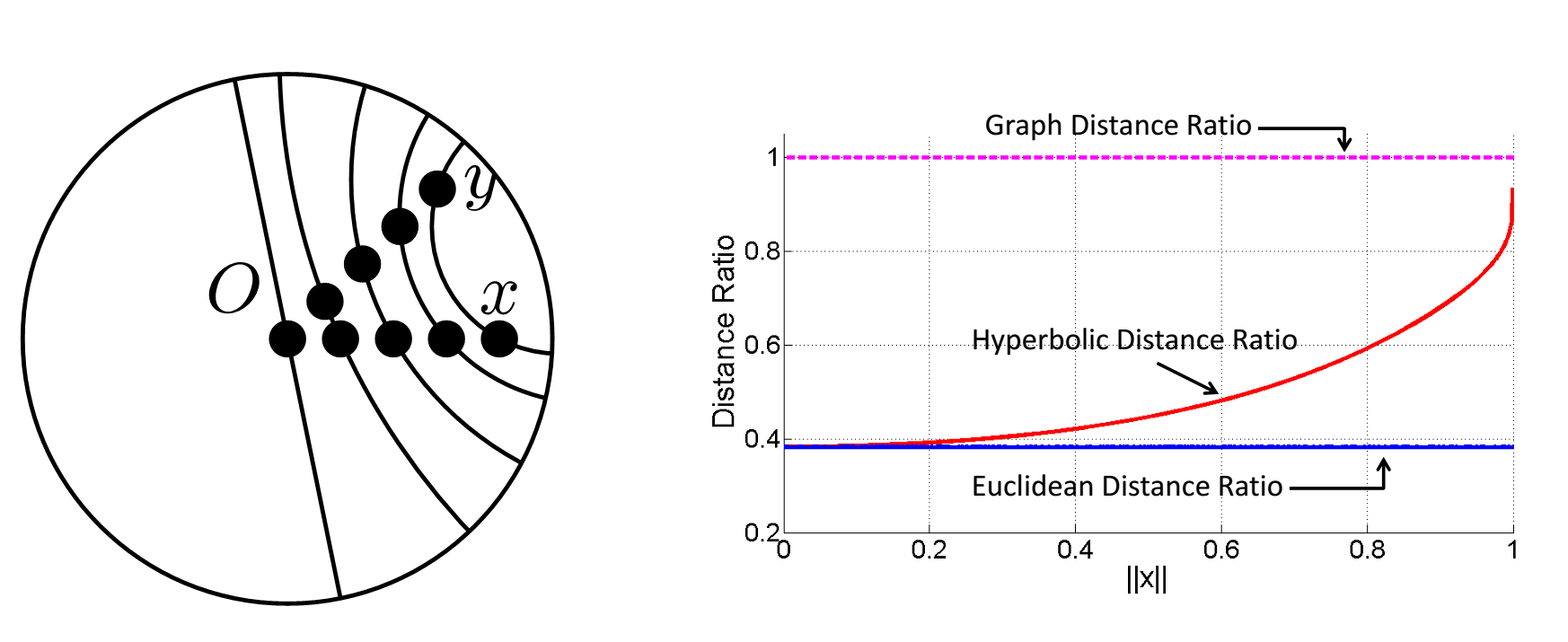
The core motivation to use hyperbolic space for embedding tree nodes is that we can mimic discrete trees. One nice example is the idea that we can reproduce an arbitrarily good approximation to tree distance, while still being in a continuous space. In a tree, the distance between a pair of siblings is 2: you have to go from one sibling to the parent and then back down. We cannot hope to approximate this behavior in Euclidean space, but we can in the hyperbolic case (and in fact building on this idea enables us to embed trees with arbitrarily low distortion, with just two dimensions!). Check out our blog post on hyperbolic geometry to understand the details behind this idea, and our ICML paper for the full picture.
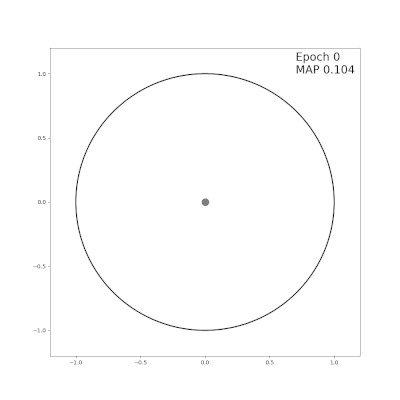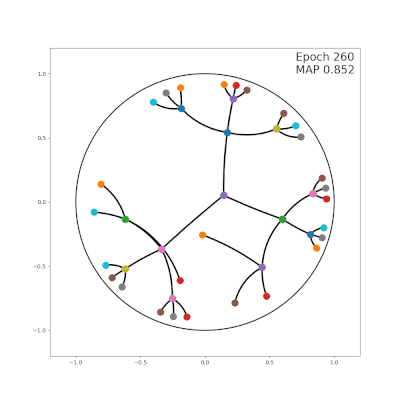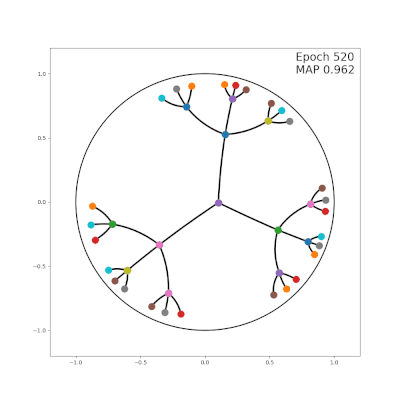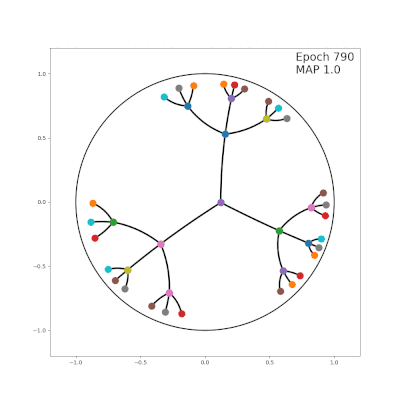
Moreover, hyperbolic space admits generalizations of important algorithms like multidimensional scaling (MDS) and principal components analysis (PCA). We also offer multiple algorithms for tree embeddings (and for other graphs!), including an algorithm based on the elegant construction of Sarkar.
While these results are surprising and can seem magical, they come at a cost. Precision (i.e., the number of bits we must use to write down our coordinates) is involved in a tradeoff between embedding fidelity, the properties of the tree (maximal degree and depth), and the embedding dimensions. Fortunately, this tradeoff is easy to characterize: numerical issues are a problem for very long chains, so that hyperbolics are great for short, bushy trees and struggle with trees with long paths.
Lots of important questions have been explored recently. Hyperbolic embeddings involve choosing a model of hyperbolic space; the disk shown above is the Poincaré disk---but other models are available. Nickel and Kiela showed how to use the Lorentz model (e.g., the hyperboloid) with easier training than their first work for the Poincaré disk. Khrulkov et al. use the Klein model to optimize their hyperbolic image embeddings.
What's the Right Space?
The standard example above had to do with hierarchies---trees---but often our data doesn't have such a nicely regimented structure. We explore this setting in our ICLR '18 paper. In fact, if we try to represent data that isn't tree-like, we can run into problems in hyperbolic space. There is a matching issue here, which is easiest to understand in terms of graph primitives:
- Trees fit hyperbolic space,
- Cycles fit spherical space (embed them around a great circle on the sphere!).
Moreover, there's lower bounds on how well we can fit either.
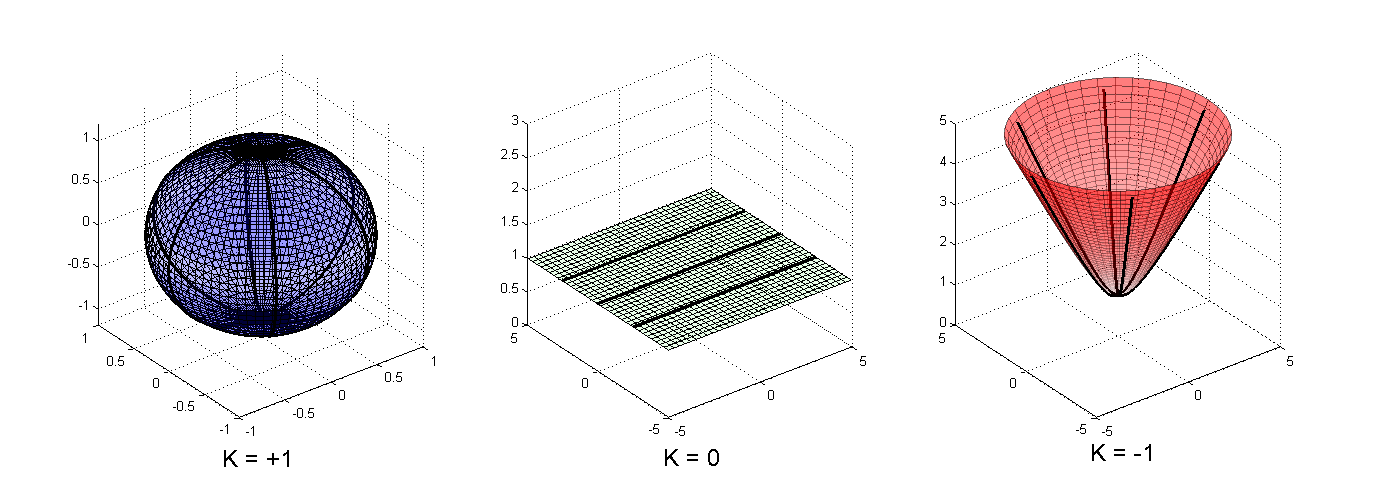
Ideally, we could hope to discover or form some more general space that matches the structure of our data. Differential geometry provides us with many tools to "glue" together spaces, but we stand to lose the simplicity and elegance of the three model spaces: hyperbolic, Euclidean, and spherical. These well-studied spaces offer simple and explicit closed-form expressions for many functions of interest: distances, \(\exp\) and \(\log\) maps, parametrizations for geodesics, etc.
In our paper, we argue that the natural tool that enables us to capture many more kinds of data while still preserving the ease-of-use of the basic spaces is the product manifold. This product is just what it sounds like: the various aspects of our manifold decompose into a product (the underlying space is the Cartesian product of base spaces, the Riemannian metric is the product of metrics, and so on). Naturally, we choose the base spaces as copies of the model spaces: hyperbolic, Euclidean, and spherical. These have curvature that is constant negative, zero, and constant positive, respectively, and the combination thus allows us to capture a flexible range of spaces.
The chief advantage of this approach is that the decomposability carries over to higher-level concepts and algorithms. For example, (the square of) distances decompose: $$d^2(p_1, p_2) = d^2_{H_1}(p_1, p_2) + d^2_{H_2}(p_1, p_2) + \ldots + d^2_{S_1}(p_1, p_2) + \ldots + d^2_{E}(p_1, p_2).$$ This also implies that training an embedding in the product space is no harder than training an embedding for one space.
As we might expect, various kinds of graphs benefit from different allocations of products---often improving on just a single Euclidean or hyperbolic space. The table below shows how distortion can be significantly reduced via combinations of spaces, like the product of two \(5\)-spheres or a \(5\)-hyperboloid and a \(5\)-sphere. Better yet, a simple heuristic algorithm lets us estimate, directly from the graph we wish to embed, how many copies of spaces and what allocations of dimensions we should give them (we call these choices the signature of the space). Recent ICLR works implement our product approach for models like GCNs and VAEs.
| Space | City Distances | CS PhDs Relationships | Power Grid | Facebook Graph |
| \(\mathbb{R}^{10}\) | 0.0735 | 0.0543 | 0.0917 | 0.0653 |
| \(\mathbb{H}^{10}\) | 0.0932 | 0.0502 | 0.0388 | 0.0596 |
| \((\mathbb{S}^5)^2\) | 0.0593 | 0.0579 | 0.0471 | 0.0658 |
| \(\mathbb{H}^5 \times \mathbb{S}^5\) | 0.0622 | 0.0509 | 0.0323 | 0.04 |
Now that we've figured out how to embed well... how do we make this useful for popular models?
Breaking the Euclidean Barrier: Improving on GCNs
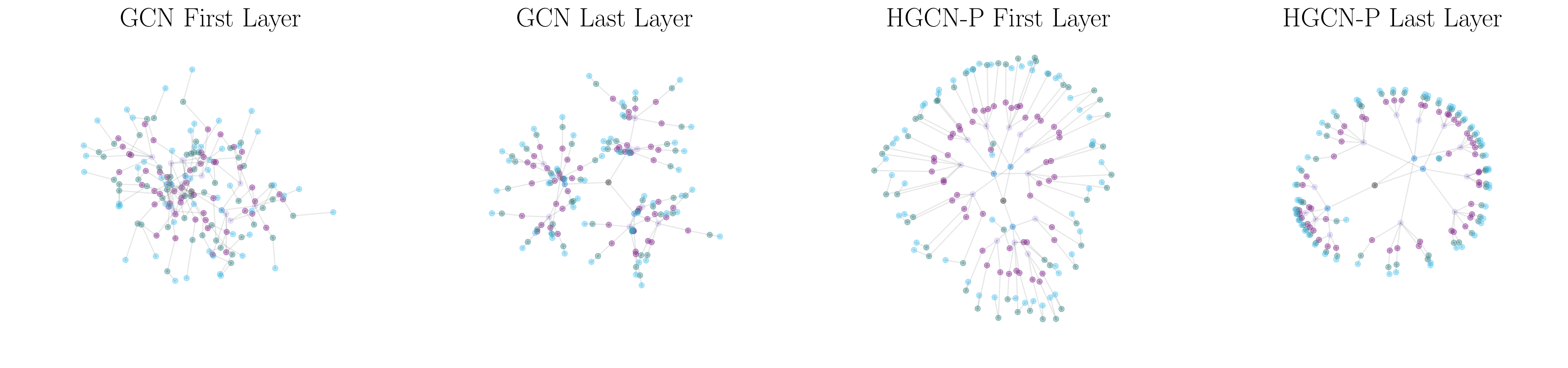
In our recent NeurIPS paper on hyperbolic graph convolutional networks (HGCN), we use non-Euclidean ideas in a popular family of neural networks, graph neural networks (GNNs). Our work develops practical techniques that can improve the predictive performance of recently-developed graph convolutional networks (GCNs) using ideas from hyperbolic geometry. We found these new hyperbolic versions of GNNs work well when the underlying graph is more hyperbolic---reaching state-of-the-art on PubMed!
GNNs not only embed structure, but also preserve semantic information that might come with the graph in the form of node features. Most GNNs models are based on a message passing algorithm, where nodes aggregate information from their neighbors at each layer in the GNN network. Generalizing message passing algorithms to non-Euclidean geometry is a challenge: we do so is by using the tangent space. Recent work leverages gyrovector theory to define useful operations in ML such as addition \(\oplus\) or matrix-vector multiplication \(\otimes\). These operations are applied in the Euclidean tangent space at the origin, and mappings from and to this space are done via the \(\exp\) and \(log\) maps. In HGCN, we use these techniques to perform message passing in hyperbolic space in a two step-process:
$$\mathbb{h}_i = W\otimes\mathbf{x}_i \oplus\mathbf{b}\ \ \text{(Feature transformation)}$$ $$\mathrm{exp}_{\mathbf{x}_i}(\sum_{j\in\mathcal{N}(i)}w_{ij}\mathrm{log}_{\mathbf{x}_i}(\mathbf{x}_j))\ \ \text{(Aggregation)}$$where \(W\) and \(b\) are model parameters, and \(w_{ij}\) are weights that can be fixed or learned with attention to capture nodes’ hierarchies. Note that the aggregation is performed at the local tangent space of each point, which better approximates the local hyperbolic geometry---giving us our performance boosts when using hyperbolic-like datasets.
New Challenges and Opportunities
As we saw, non-Euclidean geometries were introduced to serve the need for more faithful representations, and indeed, the first phase of papers focused on this goal. A clear downstream use awaited the development of non-Euclidean models that achieve state-of-the-art performance, which have just come on to the scene. These methods are full of promise, but with this comes a variety of challenges.
Perhaps the most difficult operation to lift to manifolds is the simplest in the Euclidean case: the linear transformation. Lacking a linear structure, we must find manifold analogs. In some cases, these analogs are simple: we can compute a convex combination of a pair of points by finding the appropriate point along the geodesic joining them. We can compute the mean of a set of points by computing the Karcher mean (though we have to be careful sometimes: what is the `mean` of a pair of antipodal points on the sphere?) We used these operations, for example, to lift analogy tasks to product manifolds. Other interesting analogs have been used to produce
- Hyperbolic versions of attention, by Gulcehre et al.,
- Hyperbolic word embeddings, introduced by Tifrea, Becigneul and Ganea,
- Manifold versions of structured prediction, by Rudi et al.
Many challenges remain, however. For example, is there a principled choice of analog for any particular Euclidean operation? Can we reliably and smoothly transform between spaces of varying curvature, including switching the sign?
Even further, we’d like to understand how geometry encodes relationships. A key idea is to use operations to do so---and we do so via hyperbolic rotations in our brand new work on hyperbolic knowledge graph (KG) embeddings! In this work, we explore how rotation operations---known for real and complex spaces---give us additional flexibility in hyperbolic space, enabling us to better represent knowledge, especially in hierarchical KGs.
Takeaways:
- Non-Euclidean spaces offer lots of promise for ML tasks and models,
- Hyperbolic embeddings are great for trees---and have practical algorithms and theoretical guarantees,
- Product spaces give us more flexibility for embeddings lots of types of data,
- New insights help hyperbolic GCNs achieve state-of-the-art performance,
- Many great non-Euclidean directions lie ahead!