Automatic Time Series Smoothing with ASAP
Dashboard-based visualization is critical in monitoring and diagnosing modern applications and services. However, most time-series dashboards simply plot raw data as it arrives. In a recent paper, we showed it’s possible to increase human accuracy in identifying anomalies in time series visualizations by up to 38% while reducing response time by up to 44% by adopting a simple strategy: smooth your dashboards! Moreover, our ASAP.js library will smooth your plots automatically.
As a motivating example, consider the two plots of the same time series recording the monthly temperature in England over 200 years. While the plot of the original time series is dominated by the yearly fluctuations of temperature (top plot), the smoothed plot generated by applying a 25-year moving average is able to highlight an overall increase in temperature from the 1900s (bottom plot).
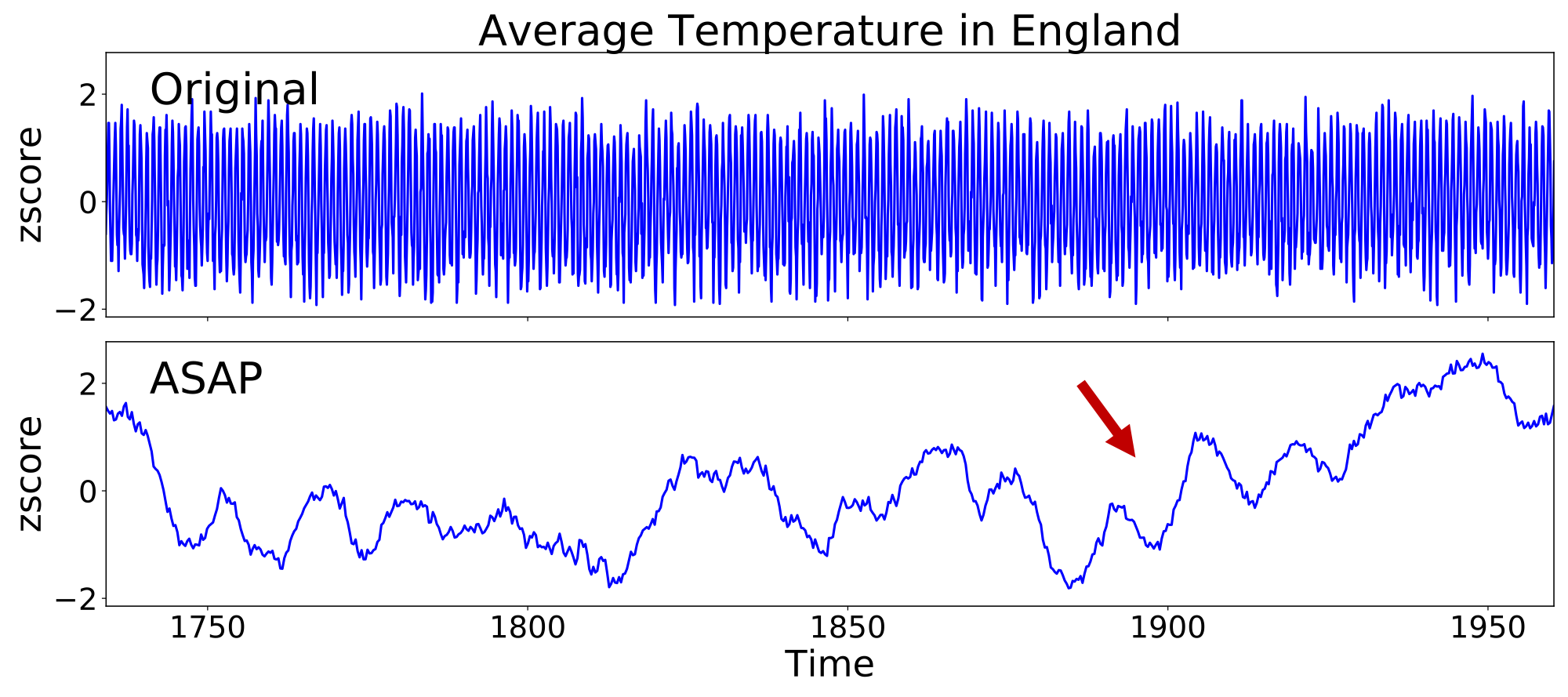
As the above example illustrates, the original plot over-represents the short-term fluctuations in the time series visualizations, obscuring the overall trend. Therefore, to automatically provide more informative visualizations like the above, we’ve created a new visualization technique called ASAP, which automatically smooths time series to remove short-term fluctuations and therefore highlight significant deviations. The key insight is to make the time series as smooth as possible while still preserving long-term deviations.
In this post, we’ll walk through an example of how ASAP chooses the amount of smoothing for a given time series and how ASAP’s strategy of minimizing point-to-point variance while preserving kurtosis can dramatically improve visualization quality. Or you can just check out the live demo and Javascript code.
Why is smoothing time series visualizations a good idea?
To assess the effect of smoothing on users’ ability to identify long-term deviations in the time series, we performed a 250-people user study on Amazon Mechanical Turk. For a set of datasets containing anomalies, we randomly presented users with a plot of either the original time series or the time series smoothed by ASAP. Below is an example dataset of taxi volume in New York city over a two-month period, during which there was an overall drop in volume during the week of Thanksgiving. We subsequently ask users to identify the region in their given time series where the drop occurred.
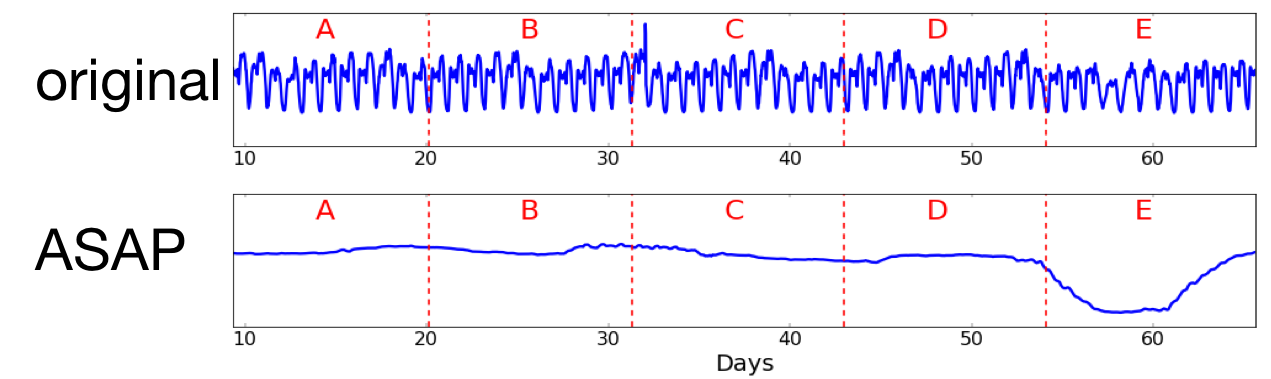
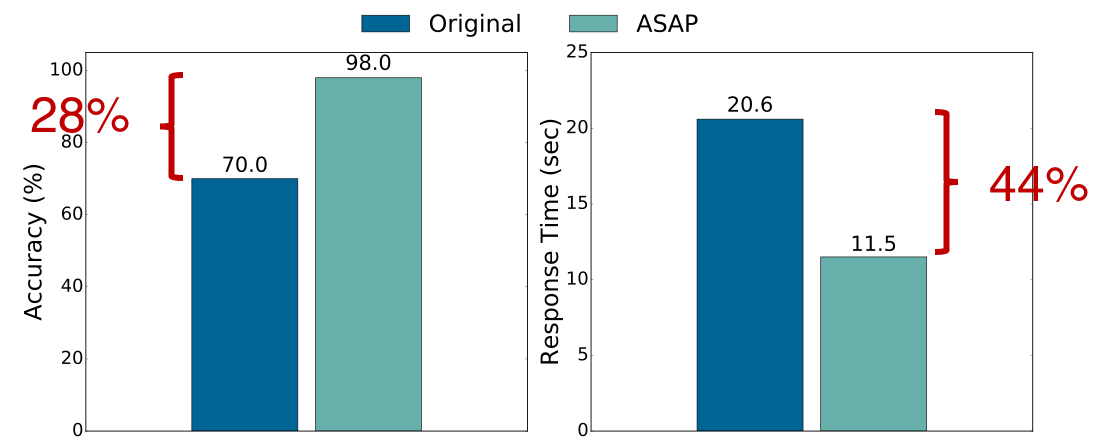
When presented with the smoothed plot instead of the raw plot, users identified the deviating region (E) 28% more often they did so 44% faster. We repeated similar experiments on four other datasets, and saw a maximum 38% (average 21%) increase in accuracy and a maximum 44% (average 24%) decrease in response time.
ASAP: Automatic Smoothing for Attention Prioritization
Given that smoothing can improve user perception of deviations in time series, how should we decide how much to smooth?
As a running example, imagine an infrastructure engineer who wants to smooth her CPU usage plot on the dashboard (left plot). How should she smooth this plot? It turns out that this is not an easy question to answer: if she smooths too little, the resulting visualization (middle plot) is still noisy; if she smooths too much, the visualization (right plot) loses structure and therefore does not provide much context regarding the potential causes of the increased usage.
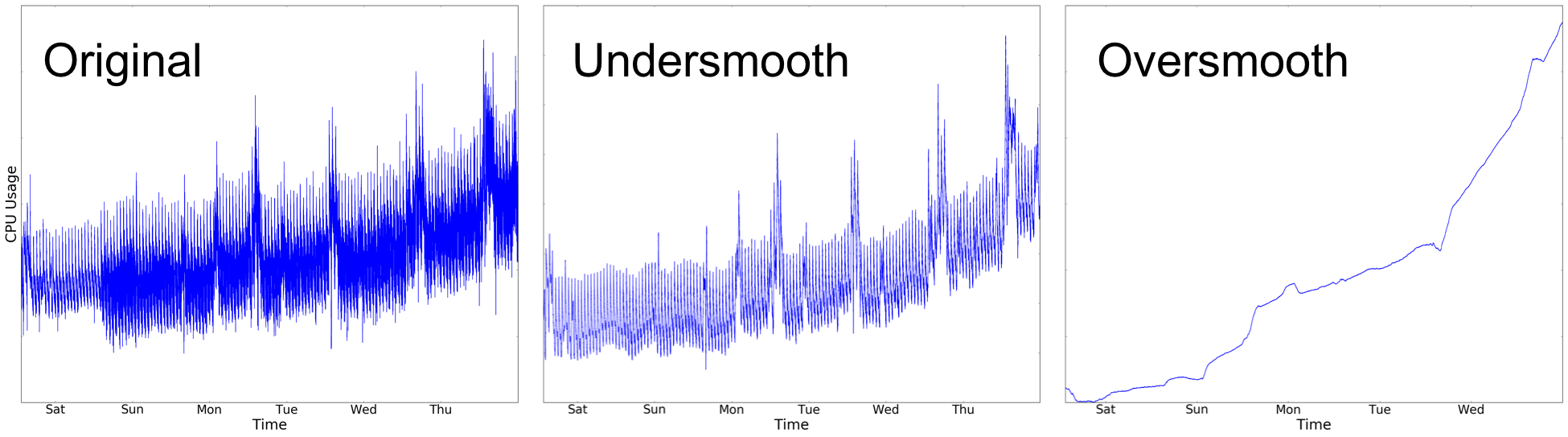
Since the amount of smoothing can have a large impact on visualization quality, we developed a new technique called ASAP, that automates the choice of smoothing parameters.
Smoothing function and smoothness measure
ASAP uses moving average as the smoothing function both because it is simple to implement and because it is effective at smoothing out short-term fluctuations (and therefore highlighting trends). We can control the amount of smoothing for the moving average by changing the window size. In general, the larger window sizes correspond to more smoothing:
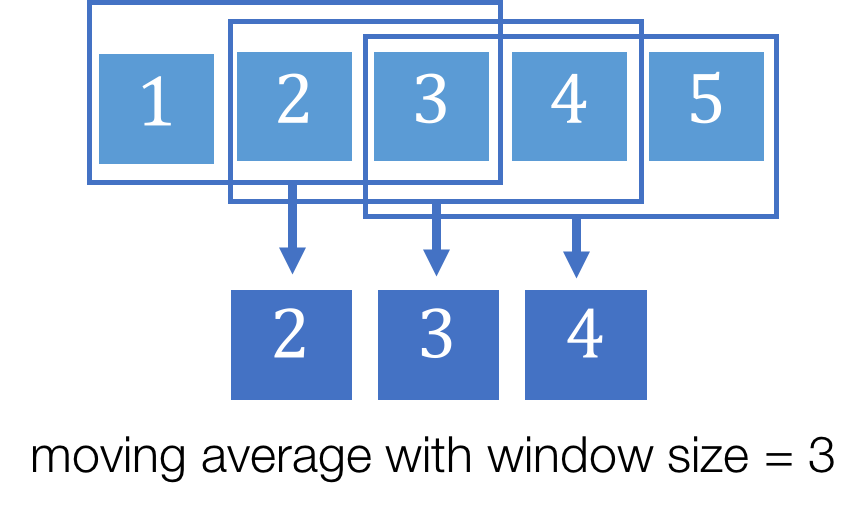
To quantitatively compare two smoothed plots, we need a metric that measures the “smoothness” of time series visualizations. Standard summary statistics (e.g. mean, variance) are a poor fit for the task, as illustrated by the two time series below, which appear visually distinct yet both have mean of zero and variance of one. The blue time series looks “smoother” than the red because there are fewer “fluctuations” between neighbouring points. In fact, the difference between neighbouring points is oscillating between 2 and -2 in the red time series, as opposed to staying at a constant of 0.7 in the blue time series.
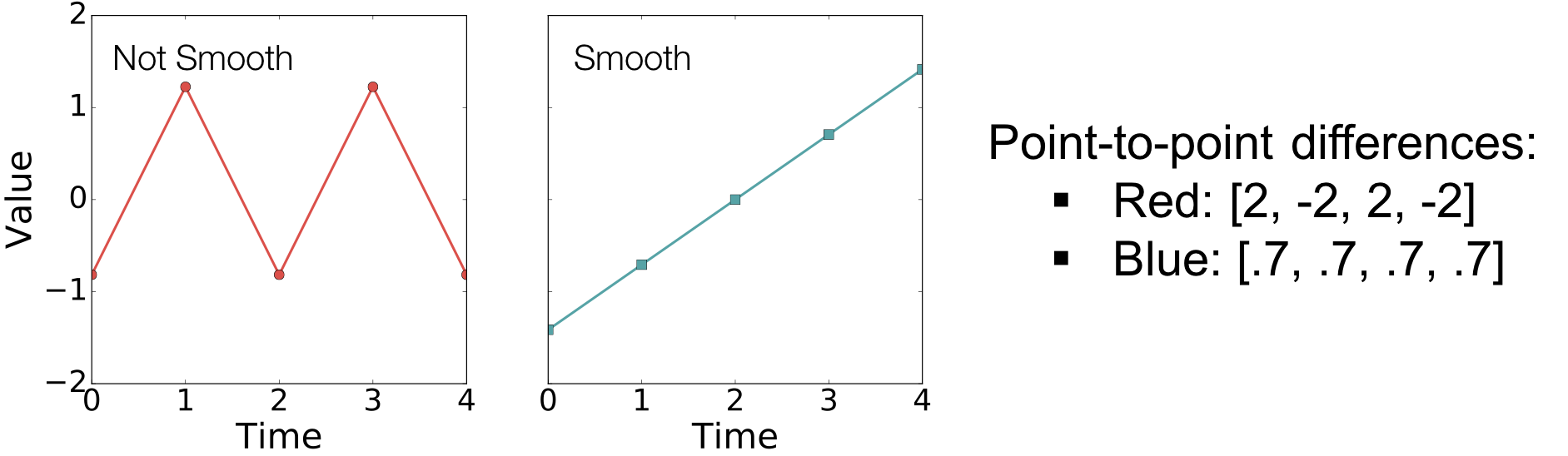
Therefore, ASAP quantifies the smoothness of a time series visualization by measuring the variation of the differences between neighbouring points. The smaller the variation, the smoother the time series. For example, the red and blue time series aforementioned have variance 4 and 0 respectively.
Preservation measure
Our smoothing strategy suggests we should increase the window size of the moving average to decrease point-to-point differences. However, if we keep smoothing, we will end up with a straight line, which is smooth but might not be interesting for users to look at. What we are missing is a means of preventing oversmoothing.
For intuition, compare the following two smoothed versions of our example CPU usage plot:
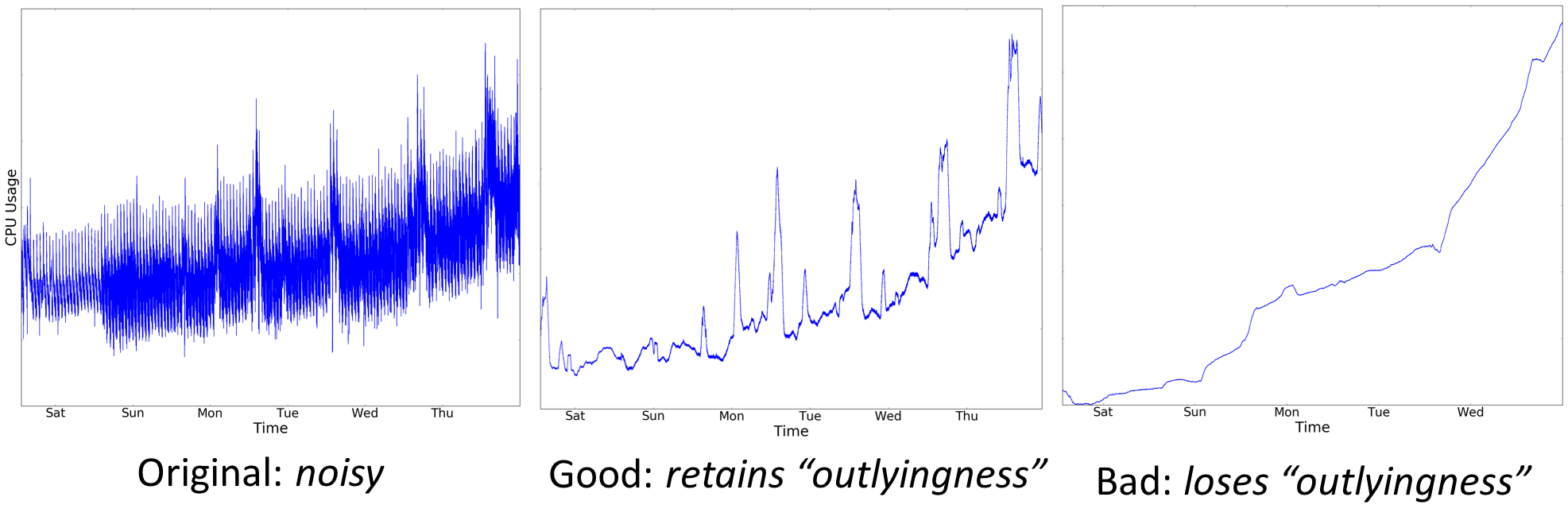
The middle plot is a good amount of smoothing since it removes the noisy fluctuations while preserving the usage spikes in the original plot, which provide context for the overall increasing trend; the right plot, in comparison, smooths away the peaks and is only left with an increasing trend.
ASAP’s strategy to prevent oversmoothing is to measure how well the smoothed plot is preserving the significant deviations, or “outlyingness” in the original plot. Conveniently, the kurtosis measure in statistics exactly captures this outlyingness of the underlying distribution that generates the time series. Informally, high kurtosis indicates that the distribution is prone to produce outliers (or infrequent extreme deviations), whereas low kurtosis indicates that the distribution is rather uniform. In the CPU usage plot example above, the original plot has kurtosis 4.1, and the “good” and “bad” smoothings have kurtosis 4.3 (> 4.1) and 2.8 (< 4.1) respectively. In ASAP, we prevent smoothing away large-scale deviations in the original time series by ensuring any smoothing preserves its kurtosis.
Putting it all together
In summary, ASAP makes time series visualizations as smooth as possible while preserving long-term deviations. Concretely, ASAP’s goal is to minimize the variance of point-to-point differences by adjusting the window size of the moving average function, while making sure that kurtosis of the smoothed time series is no smaller than that of the original time series.
Going faster
To make ASAP run at interactive speed, we employ several optimizations. For example, ASAP takes into account the resolution of the end display devices and preaggregates time series accordingly. ASAP’s smoothed time series are designed to be displayed on devices such as computer monitors, smartphones, and tablet screens for human consumption, each which has a limited resolution that is usually much smaller than the dimensionality of a given time series. These pixel densities place restrictions on the amount of information that can be shown in a plot. For example, there is little benefit in plotting all 10K points in a time series displayed on iPhone 7, which only has a resolution of 1334 pixels. Therefore, ASAP preaggregates time series according to the available resolution on the end device to save computation.
We have two more advanced strategies in the paper, which prune computation for periodic data (by measuring autocorrelation) and avoid materializing visualization updates faster than humans can see (e.g., 30 times a second, even if time series are arriving much faster).
Conclusions
In summary, short-term fluctuations in time series visualizations can often obscure the overall trends. ASAP is a technique for automatically making time series as smooth as possible while preserving long-term deviations. ASAP quantifies the visual smoothness of the time series using the variance of point-to-point differences, and preserve significant deviations in the plot by preserving kurtosis. ASAP employs optimizations such as pushing down the resolution constraints of physical devices to the algorithm to achieve interactive speeds. Our paper, appearing in VLDB this month, contains more details of the algorithm, optimizations and performance and user study results. And you can also try our ASAP Javascript library from the demo website.